Locus of a Point from a Parabolic Function

By

Cassian Mosha

Problem:

Consider the locus of the vertices of the set of parabolas graphed from show that the locus is the parabola where a=1

Solution:

Let’s consider , and a=1. Also let’s consider Now let’s try to draw the graphs from the limit we set up in the equation for values of b.

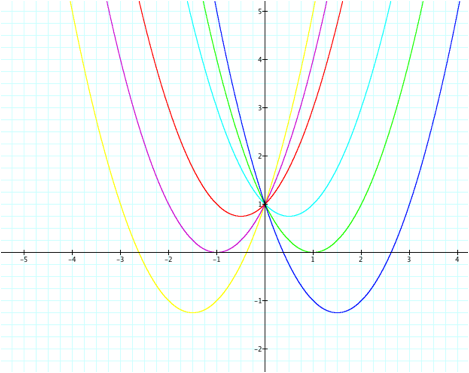
Graph #1

With the graphs we can find the minimum values of the graphs, and in this case it will be only the x-values that corresponds to the vertex values. The easiest way to do this is by using differentiation to find the minimums. So dy/dx of is 2ax+b. Setting the derivative equal to zero, and since a=1, we can find that the minimum value of the expression and it is x=-b/2a.

Now let’s try to plug in the value of x we found above using derivatives to the original equation and see what happens.. This is represented on every of our graphs as shown above, and so we can find the minimum value of y which is , and so the vertex of every graph we displayed above is .

Now let’s consider the other graph we depicted above that is . What will happen if we graph this equation on the same set of axes as we did before?

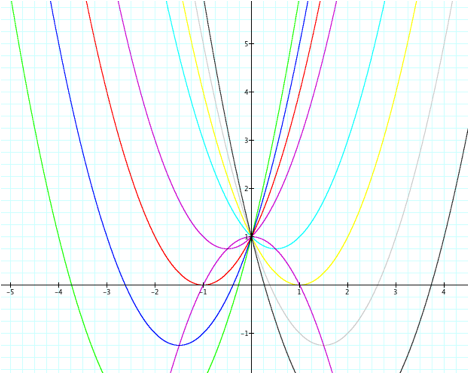
Graph #2

As we can see the h(x) parabola turns upside down, share common y-intercept point with the other graphs, and it intersects all other graphs at its vertex. Now let's set both equations equal to each other, solve for b again as we did for the f(x) and see what happens. . Since a=1 we can solve for b by collecting like terms and simplify, and that is . Now if we substitute this value of x into the equation of h(x) we get which points into the minimum value of each of our f(x) functions for the values of b from -4 to 4. Hence we can conclude that we have shown that the locus of with a=1 can be shown by the function with a=1 also.

Return